Piotr Błaszczyk
Między Escherem a della Francesca
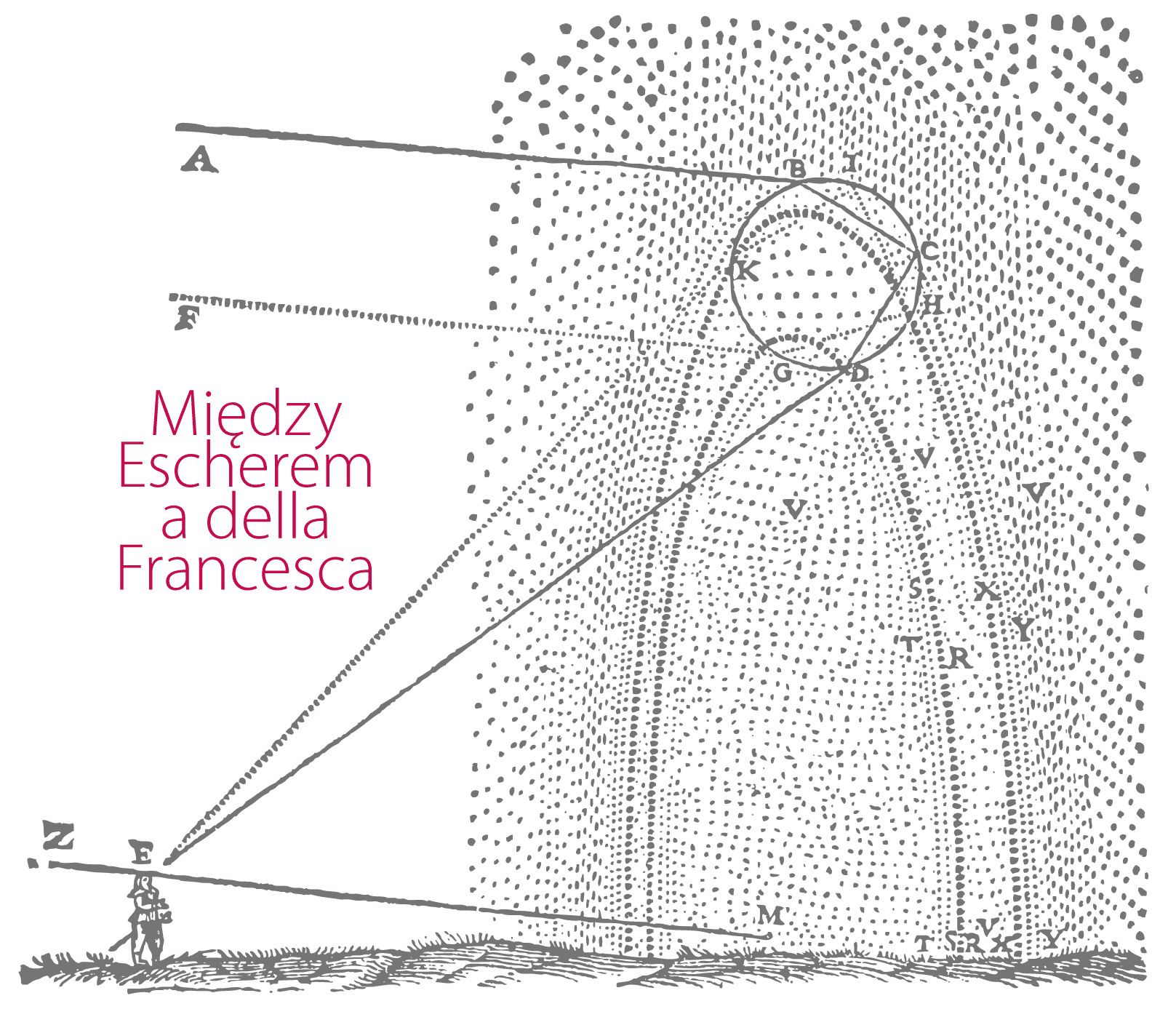
Pierwsze twierdzenia Elementów Euklidesa w zaskakujący sposób rozwijają geometrię neutralną, czyli to, co jest prawdziwie w świecie euklidesowym i hiperbolicznym. Dopiero gdy w twierdzeniu 29-tym zastosowany zostanie Piąty Postulat wykład rozwija się w sposób dobrze wszystkim znany, z trójkątami, w których kąty sumują się do dwóch kątów prostych, z kwadratami i twierdzeniem Pitagorasa, figurami podobnymi i proporcjami odcinków. Pamiętamy to ze szkoły niczym pacierz. Na początku XIX wieku kilku odważnych pokazało, że możliwe są przestrzenie, w których nie ma kwadratów, a kąty trójkąta nie sumują się do pi. Ten dziwny świat wprowadził do swoich grafik Maurits Escher. Jego prace z lat 50-tych bezpośrednio nawiązują do modelu geometrii hiperbolicznej, który Henri Poincaré podał jeszcze w XIX wieku. Drugi, nawet bardziej spektakularny przykład bezpośredniego zaangażowania geometrii w sztukę wiąże się z malarstwem Piero della Francesca. Oczywiście wielu Renesansowych artystów wykorzystywało złoty podział, kompozycje oparte na pięciokącie foremnym, itp. Della Francesca jednak obok tego, że studiował Elementy i Optykę Euklidesa, był też twórczym matematykiem. Jego twierdzenie 1.13 z O perspektywie w malarstwie stanowi osnowę kompozycji Biczowania Chrystusa.
Geometria w obrazach Barok, Dopamina i Meteory nie występuje ani jako przedstawienie, nie jako podstawa kompozycji – wyrasta z zauroczenia drzeworytami ilustrującymi eseje naukowe Kartezjusza.
W ostatnich latach literatura polska zyskała nowe przekłady Elementów Euklidesa, księgi V- VI, oraz Geometrii i Dioptryki Kartezjusza. Katarzyna Kopańska uczestniczyła w tych edycjach jako grafik. Obrazy z serii Barok, Dopamina i Meteory są inspirowane jej udziałem w projekcie Kartezjusz.
Rozprawa o metodzie Kartezjusza składa się z tytułowej rozprawy filozoficznej i trzech esejów: Meteory, Dioptryka, Geometria. Każda z tych prac przynosi epokowe odkrycie. Meteory zawierają pierwsze naukowe wytłumaczenie zjawiska tęczy. W Dioptryce Kartezjusz wyprowadza prawo załamania światła. Geometria nie zawiera co prawda jakiegoś jednego wyjątkowego osiągnięcie, ale prezentuje zupełnie nowy język, nowy sposób uprawiania matematyki tak, iż można powiedzieć, że cała nowożytna matematyka wywodzi się z Geometrii. To co urzekło Katarzynę to nie osiągnięcia naukowe, a drzeworyty ilustrujące eseje naukowe.
Geometria Euklidesa budowała w malarstwie renesansowym perspektywę malarską, porządek i ciszę obrazu. Kartezjusz przynależy do paradygmatu euklidesowego tylko formalnie. Oglądany przez pryzmat drzeworytów, jego świat jest w ruchu, pełen wirów i obrotów. Mamy więc w Geometrii zagęszczenia przecinających się okręgów, elipsy, parabole i machiny kreślące krzywe algebraiczne coraz to wyższych rzędów.
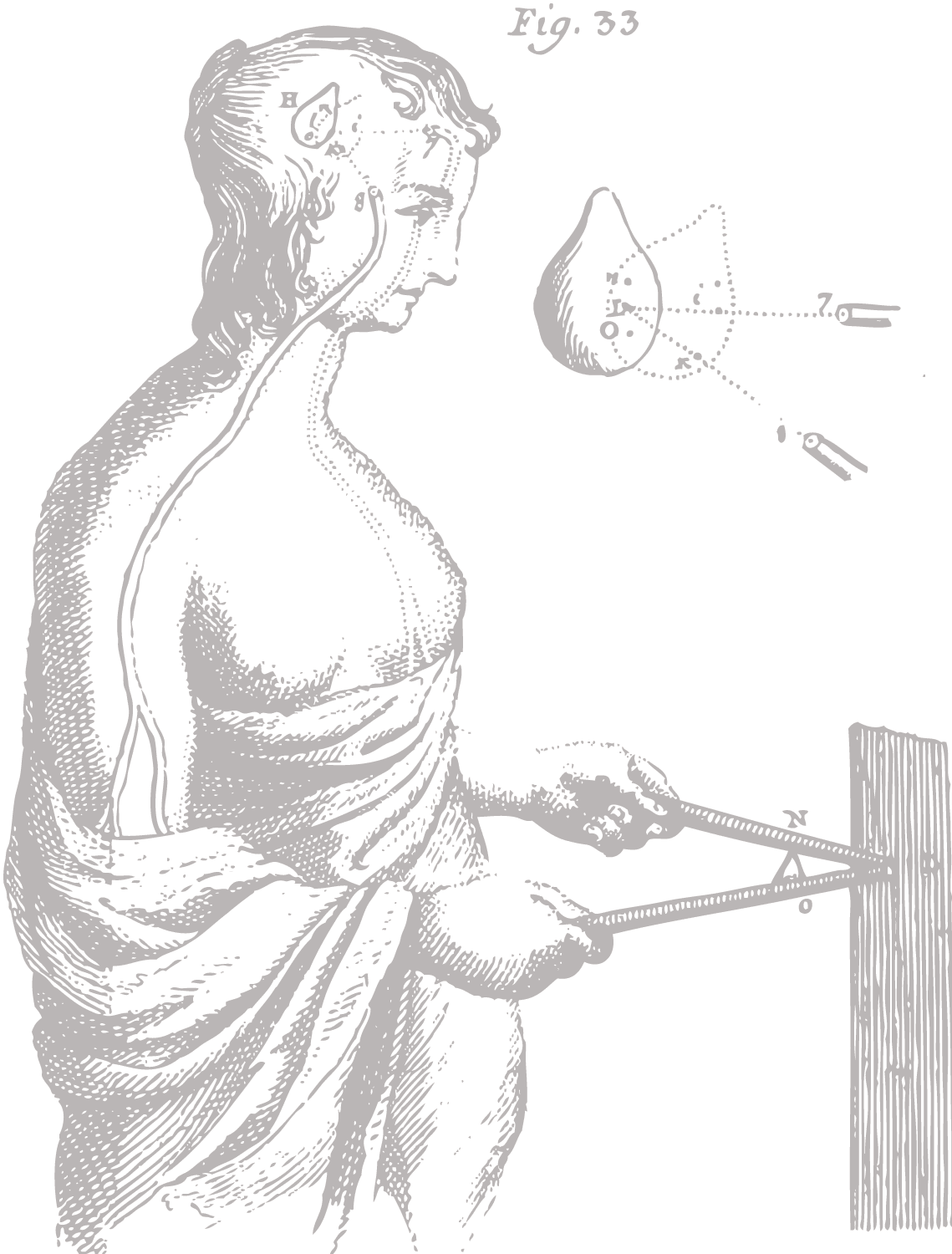
Nowe, nieznane Grekom krzywe składają się z przecięć innych krzywych i rozpadają się na punkty. W Dioptryce przedstawienia nie są już tak abstrakcyjne. Mamy tu więc projekty lunet, które konstruowane w oparciu prawo załamania miały przynieść Kartezjuszowi fortunę. Plany tokarek do szlifowania soczewek eliptycznych i hiperbolicznych. Anatomiczne przedstawienia oka i jego połączeń z mózgiem.
Mamy obraz chłopca z rakietą, bo odbiciem piłki tenisowej tłumaczy Kartezjusz prawo odbicia światła. W Meteorach zaś znajdujemy tęczę szybującą w niebo, zwieńczoną kroplą, w której promienie słońca załamują się i odbijają zgodnie z nowo-odkrytym prawem. Mamy też przedstawienie burzy, deszczu i innych zjawisk podniebnych. A wreszcie faktury różnokształtnych komórek ściśniętych do granic możliwości dłuta żłobiącego matrycę. Kartezjusz był bowiem przekonany, że różnice jakościowe w świecie sprowadzają się do kształtów, mas i ruchów przylegających do siebie cząsteczek elementarnych, bo w świecie nie ma próżni. Wszystkie te przedstawienia połączone jeszcze ze strojami epoki, koronkami, kryzami, pióropuszami w kapeluszach przepływają strumieniami przez obrazy z serii Barok, Dopamina i Meteory.
I tak, w obrazie Barok, Dopamina i Meteory błękitny, nagi młodzieniec przeskakuje od jednej do drugiej paraboli sześciennej Kartezjusza. Postać dziewczyny zamkniętej w zielonej niszy przywołuje eksperymenty anatomiczne opisane przez Kartezjusza słowami: weź oko dopiero zmarłego człowieka, lub z braku to wołu. W tle zaś kurtyna cząsteczek elementarnych fizyki kartezjańskiej dopełniająca charakterystyczny dla wielu obrazów tej serii horror vacui.
Dobry letni deszcz to wyimaginowany spór o pierwszeństwo odkrycia między Kartezjuszem i Snellem. Powszechnie, z wyjątkiem Francji, temu drugiemu przypisuje się odkrycie prawa załamania światła. Scena rozgrywa się w zasięgu zgeometryzowanej tęczy lub paraboli sześciennej, po której krążą krople wody i refleksy promieni. Młoda dziewczyna w zielonym stroju plażowym jest tu bezpieczna. Nikt nie poddaje jej eksperymentom – w goglach VR przemierza spokojnie świat Baroku.
W Dyfrakcji znajdujemy postać tenisisty z pierwszych kart Dioptryki. To przedstawienie wyraźnie nawiązuje do legendy zwierciadła, którym tak zdołano skupić promienie słońca, że jeden z rzymskich statków zmierzających na podbój Syrakuz stanął w ogniu. To przemyślne zwierciadło miało być zaprojektowane przez Archimedesa. W łodzi na obrazie zamiast Rzymian znajdujemy Ledę i Zeusa wcielonego w kilka łabędzi. Być może optyka jest tu alegorią podglądania. Trzy kolorowe elipsy sugerują filtry teatralnych reflektorów. W tym świecie jednak czerwony, niebieski i zielony nie sumują się do bieli.
W Tańcząca dziewczyna i biały pies dziewczyna ćwiczy kroki jazzowego tańca. Wirujące krzywe zgadzają się raczej z synkopami niż promieniami światła. W tle rozpoznajemy industrialną okolicę uniwersytetu OsloMet. Spacerowy nastrój przypomina wakacyjne ogrody Nationaltheatret.
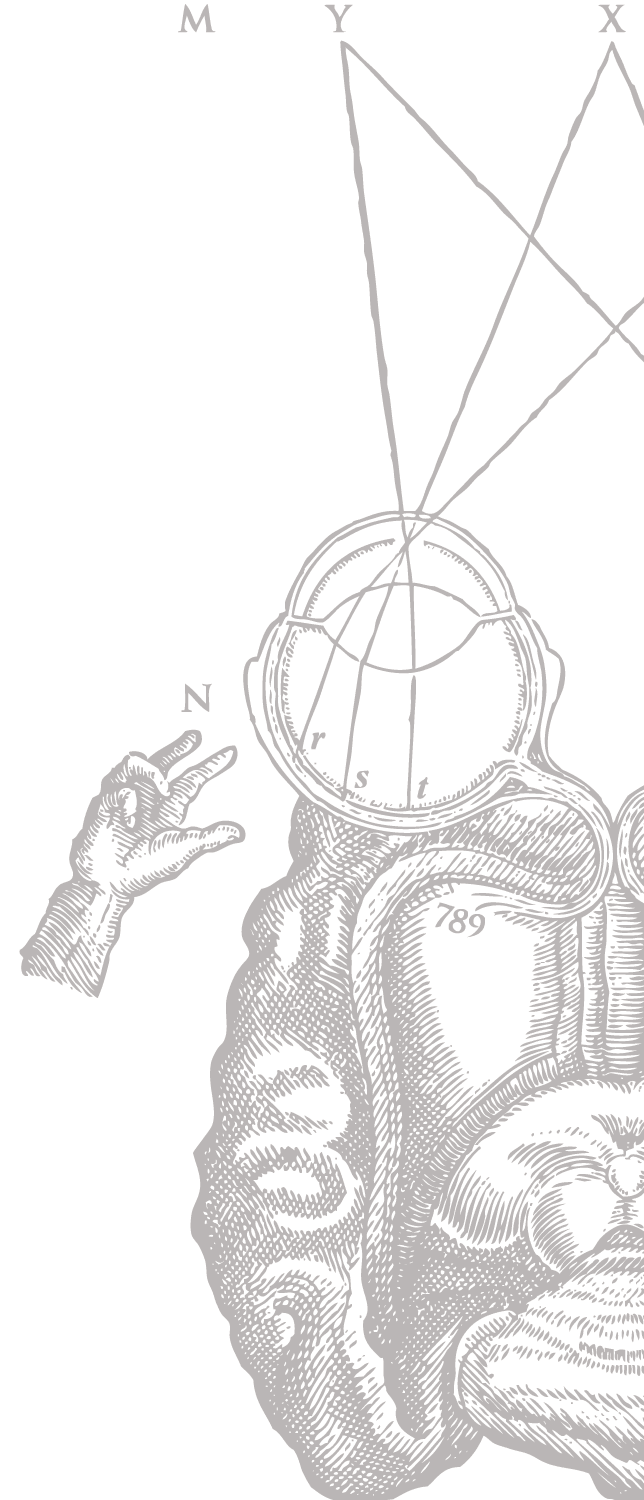
Kawaler patrzący przez lunetę to synteza kartezjańskiej optyki: teoria widzenia wypracowana przez Keplera uzupełniona o prawo załamania, twierdzenia Apoloniusza o ogniskach elipsy i hiperboli użyte do modelowania przebiegu promieni w lunecie. Ilustracja z dziewiątej rozprawy Dioptryki umieszczona jest tu w gałce ocznej przedstawionej jako soczewka. Wzrok – jak uczył Lorenz – to podstawowy zmysł ludzi i ptaków. Kawaler uzbrojony w lunetę mierzy daleko poza horyzont, zaś lekko-namalowany flaming ironicznie zerka poza obraz.
W Patrzę na Ciebie młodzieniec celując astrolabium w gwiazdy trafia na piękną kobietę. Widzimy jej szczegóły anatomiczne, zwłaszcza szyszynkę, gdzie – jak wierzył Kartezjusz – mieści się dusza. To raczej zjawa niż realna postać. Dziewczyna kieruje w serce chłopca narzędzie, które Kartezjusz opisał jako wspomagające niewidomych. Pasek CMYK na krawędzi obrazu dopełnia teatralność tej sceny.
La tempesta del mio cor (Burza w moim sercu) to słowa z arii hrabiego di Luna z drugiego aktu Il Trovatore. Nastrój obrazu kontrastuje z dramatem, który zaraz się rozegra na scenie. Na pierwszym planie Śmiejący się kawaler Fransa Halsa. Dalej, alegoria burzy szybująca nad spokojnym morzem. Pieśń Verdiego ewokuje tu przyjemność muzyki, a nie porywczość bohaterów opery.
W Tęcza Kartezjusza grafika z siódmej rozprawy Meteorów została ubrana w fizyczne barwy. Druga część obrazu jest bardziej malarska: zamknięta w owalu zieleni oliwkowej burza, a dalej, poza granicami linii geometrycznych, smugi różu weneckiego przykrywające słońce. Drobna postać Kartezjusza zarzuca na to wzmożenie przyrody sieć linii zrozumiałych tylko dla geometry.
Dr hab. Piotr Błaszczyk – matematyk i filozof, profesor w Instytucie Matematyki Uniwersytetu Pedagogicznego w Krakowie.
